Recently, Professor Chaoping Xing - the leader of the Institute of Information Security and Cryptology at School of Cyber Science and Engineering (CSE), and his collaborator Professor Venkatesan Guruswami - a visiting professor at School of CSE, have made a significant breakthrough in the area of list decoding. Their work, titled as “Optimal rate list decoding over bounded alphabets using algebraic-geometric codes”, has been accepted to the Journal of the ACM, one of the few top journals in the area of Computer Science. 

Journal of ACM is ranked Class A in the list recommended by China Computer Federation. The scope of research covered encompass contributions of long-lasting value to any area of computer science. To be accepted, a paper must be judged to be truly outstanding in its field. The work done by Professor Xing and Professor Guruswami has solved one of the open questions in list decoding. They constructed two classes of algebraic code families which are efficiently list decodable with small output list size over nearly-optimal alphabets.    

List decoding has important application to information security. In our real life, errors may be introduced when some message is transmitted over a noisy channel. Thus, the message received is no longer the message sent. List decoding helps in this situation by encoding the message before transmitting it and outputting a list containing the original message after receiving some errored message.   

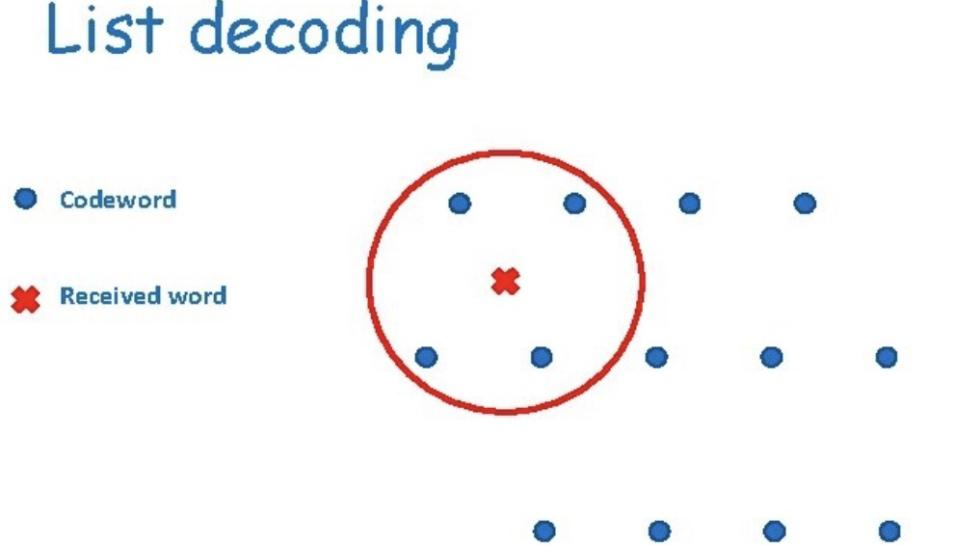
In practice, we would like to have small alphabet size and list size for a list decoding capable of correcting up to r errors so as to achieve low computational complexity and efficient decoding rate. In theory, the alphabet size and list size are lower bounded. In other words, the closer to the lower bounds, the better a list decoding is. 

Prior to this work, however, all constructions of codes for list decoding are far away from the lower bounds. They either have long alphabet size, some of which may even depend on the length of the code, or have exponential list size. It remains open to construct a code for list decoding achieving those lower bounds. 

This work solves the above challenge by constructing two classes of algebraic code families which are highly efficient to list decode. More importantly, the alphabet sizes of those two classes of codes are only a constant factor away from the lower bound, which is almost optimal. In addition, the code family in the first class has excellent list size except that the construction is not explicit. The parameters in both constructions are quite close to the existential bounds in all three aspects - error correction radius, alphabet size, and list size -simultaneously. These are the best code families for list decoding so far. 

Paper Link：https://arxiv.org/abs/1708.01070